在 XAML 中,我们对一个 UIElement 进行一个 RenderTransform 是再常见不过的事情了,我们可以从众多叠加的 TransformGroup 瞬间得到一个 Matrix 表示整个变换的综合变换矩阵,然而反过来却不好做——从变换矩阵中反向得到变换分量。
首先明确的是,各种 TranslateTransform、ScaleTransform、RotateTransform 到 Matrix 具有唯一确定的解,然而反向转换却是有无穷多个解的。于是如果我们要得到一个解,我们需要给定一个条件,然后得到这个条件下的其中一个解。
准备工作
为了写出一个通用的变换方法来,我准备了一个测试控件,并为它随意填写一个变换:
1
2
3
4
5
6
7
8
9
10
11
<Border x:Name="DisplayShape" Background="#FF1B6CB0" Width="200" Height="100">
<UIElement.RenderTransform>
<TransformGroup>
<ScaleTransform ScaleX="0.8" ScaleY="2"/>
<SkewTransform/>
<RotateTransform Angle="-48.366"/>
<TranslateTransform x:Name="TranslateTransform" X="85" Y="160"/>
</TransformGroup>
</UIElement.RenderTransform>
<TextBlock Foreground="{media:LuminanceForeground TargetName=DisplayShape}" Text="walterlv" HorizontalAlignment="Center" VerticalAlignment="Center"/>
</Border>
▲ LuminanceForeground 的作用可参见我的另一篇文章:计算能在任何背景色上清晰显示的前景色

▲ 一个随便应用了一个变换的控件
我们将从这个控件中取得变换矩阵 Matrix,然后计算出变换分量的一个解,应用到新的控件上:
1
<Rectangle x:Name="TraceShape" Width="200" Height="100" Stroke="#FFE2620A" StrokeThickness="4"/>
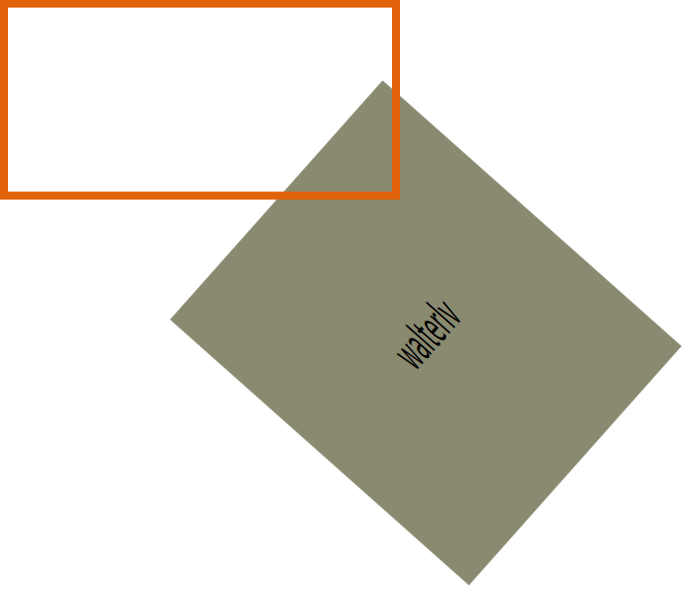
▲ 我们希望计算一组变换分量以便让这个框追踪变换了的控件
于是,我们写下了测试代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private void OnLoaded(object sender, RoutedEventArgs args)
{
var matrix = DisplayShape.RenderTransform.Value;
var (scaling, rotation, translation) = ExtractMatrix(matrix);
var group = new TransformGroup();
group.Children.Add(new ScaleTransform {ScaleX = scaling.X, ScaleY = scaling.Y});
group.Children.Add(new RotateTransform {Angle = rotation});
group.Children.Add(new TranslateTransform {X = translation.X, Y = translation.Y});
TraceShape.RenderTransform = group;
}
private (Vector Scaling, double Rotation, Vector Translation) ExtractMatrix(Matrix matrix)
{
// 我们希望在这里写出一个方法,以便得到三个变换分量。
}
OnLoaded 是为了让代码运行起来,而 ExtractMatrix 才是我们的核心——将变换分量解构出来。
思路和初步成果
我们的思路是创造一个单位矩形,让它应用这个变换,然后测量变换后矩形的宽高变化,角度变化和位置变化。由于直接使用 Rect 类型时无法表示旋转后的矩形,所以我们直接使用四个顶点来计算,于是我们写出如下代码:
1
2
3
4
5
6
7
8
9
10
11
private (Vector Scaling, double Rotation, Vector Translation) ExtractMatrix(Matrix matrix)
{
var unitPoints = new[] {new Point(0, 0), new Point(1, 0), new Point(1, 1), new Point(0, 1)};
var transformedPoints = unitPoints.Select(matrix.Transform).ToArray();
var scaling = new Vector(
(transformedPoints[1] - transformedPoints[0]).Length,
(transformedPoints[3] - transformedPoints[0]).Length);
var rotation = Vector.AngleBetween(new Vector(1, 0), transformedPoints[1] - transformedPoints[0]);
var translation = transformedPoints[0] - unitPoints[0];
return (scaling, rotation, translation);
}
运行后,我们发现追踪框已经与原始控件完全贴合,说明计算正确。

▲ 追踪框完全贴合
可以灵活应用计算结果
不过如果真要在产品中做追踪框,肯定不能像上图那样被严重拉伸。所以,我们把缩放分量去掉,换成尺寸变化:
1
2
3
4
5
6
7
8
9
10
11
private void OnLoaded(object sender, RoutedEventArgs args)
{
var matrix = DisplayShape.RenderTransform.Value;
var (scaling, rotation, translation) = ExtractMatrix(matrix);
var group = new TransformGroup();
TraceShape.Width = DisplayShape.ActualWidth * scaling.X;
TraceShape.Height = DisplayShape.ActualHeight * scaling.Y;
group.Children.Add(new RotateTransform {Angle = rotation});
group.Children.Add(new TranslateTransform {X = translation.X, Y = translation.Y});
TraceShape.RenderTransform = group;
}
以上代码中,ScaleTransform 已经被去掉,取而代之的是宽高的设置。

▲ 没有被拉伸的追踪框
更通用的方法
以上虽然达到了目的,不过实际应用中可能会有更多的限制,例如:
- 变换中心不是
(0, 0) - 最终应用的顺序不是
Scale->Rotate->Translate
首先来解决变换中心的通用性问题。
我们将变换中心设为 (0.5, 0.5):
1
<Rectangle x:Name="TraceShape" Width="200" Height="100" Stroke="#FFE2620A" StrokeThickness="4" RenderTransformOrigin="0.5 0.5"/>
于是,追踪框不知道飞到哪里去了……
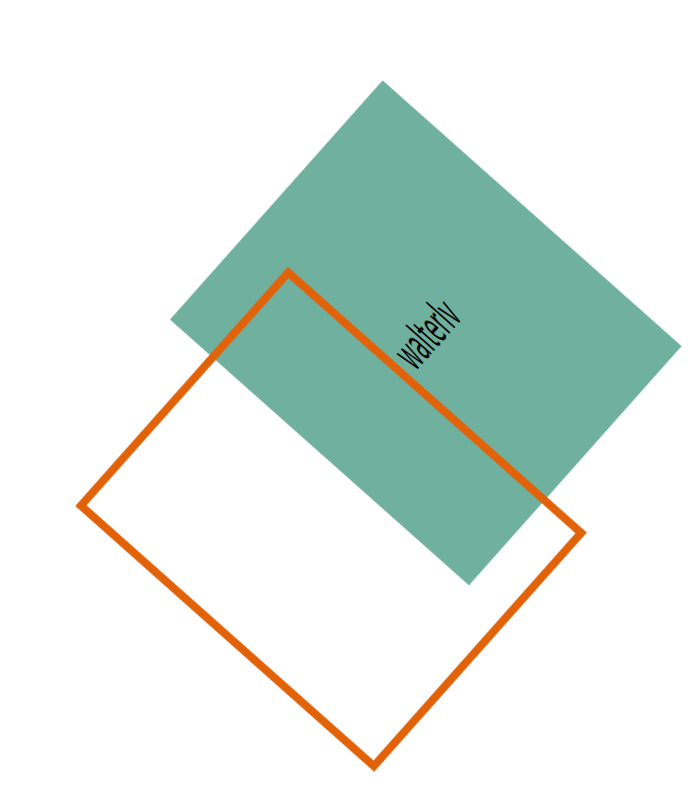
▲ 改变了变换中心
这时,我们需要将变换中心导致的额外平移量考虑在内。
如果 S 表示所求变换的缩放分量,R 表示所求变换的旋转分量,T 表示所求变换的平移分量;M 表示需要模拟的目标矩阵。那么,S 将可以通过缩放比和参数指定的缩放中心唯一确定;R 将可以通过旋转角度和参数指定的旋转中心唯一确定;T 不能确定,是我们要求的。
由于我们按照缩放->旋转->平移的顺序模拟 M,所以:
\[SRT=M\]即:
\[T=S^{-1}R^{-1}M\]所以,我们在上面的之前成果的代码上再做些额外的处理,加上以上公式的推导结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static (Vector Scaling, double Rotation, Vector Translation) MatrixToGroup(Matrix matrix, CenterSpecification specifyCenter = null)
{
// 生成一个单位矩形(0, 0, 1, 1),计算单位矩形经矩阵变换后形成的带旋转的矩形。
// 于是,我们将可以通过比较这两个矩形中点的数据来求出一个解。
var unitPoints = new[] {new Point(0, 0), new Point(1, 0), new Point(1, 1), new Point(0, 1)};
var transformedPoints = unitPoints.Select(matrix.Transform).ToArray();
// 测试单位矩形宽高的长度变化量,以求出缩放比(作为参数 specifyCenter 中变换中心的计算参考)。
var scaling = new Vector((transformedPoints[1] - transformedPoints[0]).Length, (transformedPoints[3] - transformedPoints[0]).Length);
// 测试单位向量的旋转变化量,以求出旋转角度。
var rotation = Vector.AngleBetween(new Vector(1, 0), transformedPoints[1] - transformedPoints[0]);
var translation = transformedPoints[0] - unitPoints[0];
// 如果指定了变换分量的变换中心点。
if (specifyCenter != null)
{
// 那么,就获取指定的变换中心点(缩放中心和旋转中心)。
var (scalingCenter, rotationCenter) = specifyCenter(scaling);
// 如果 S 表示所求变换的缩放分量,R 表示所求变换的旋转分量,T 表示所求变换的平移分量;M 表示传入的目标矩阵。
// 那么,S 将可以通过缩放比和参数指定的缩放中心唯一确定;R 将可以通过旋转角度和参数指定的旋转中心唯一确定。
// S = scaleMatrix; R = rotateMatrix.
var scaleMatrix = Matrix.Identity;
scaleMatrix.ScaleAt(scaling.X, scaling.Y, scalingCenter.X, scalingCenter.Y);
var rotateMatrix = Matrix.Identity;
rotateMatrix.RotateAt(rotation, rotationCenter.X, rotationCenter.Y);
// T 是不确定的,它会受到 S 和 T 的影响;但确定等式 SRT=M,即 T=S^{-1}R^{-1}M。
// T = translateMatrix; M = matrix.
scaleMatrix.Invert();
rotateMatrix.Invert();
var translateMatrix = Matrix.Multiply(rotateMatrix, scaleMatrix);
translateMatrix = Matrix.Multiply(translateMatrix, matrix);
// 用考虑了变换中心的平移量覆盖总的平移分量。
translation = new Vector(translateMatrix.OffsetX, translateMatrix.OffsetY);
}
// 按缩放、旋转、平移来返回变换分量。
return (scaling, rotation, translation);
}
本来第二个参数是可以用 Func 的,但那样的意义解释起来太费劲,所以改成了委托的定义:
1
2
3
4
5
6
/// <summary>
/// 为 <see cref="MatrixToGroup"/> 方法提供变换中心的指定方法。
/// </summary>
/// <param name="scalingFactor">先进行缩放后进行旋转时,旋转中心的计算可能需要考虑前面缩放后的坐标。此参数可以得知缩放比。</param>
/// <returns>绝对坐标的缩放中心和旋转中心。</returns>
public delegate (Point ScalingCenter, Point RotationCenter) CenterSpecification(Vector scalingFactor);
这时我们就可以得到我们想要的 TransformGroup,而且 RenderTransformOrigin 随便设:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
private void OnLoaded(object sender, RoutedEventArgs args)
{
var matrix = DisplayShape.RenderTransform.Value;
var (scaling, rotation, translation) = TransformMatrix.MatrixToGroup(matrix,
scalingFactor => (new Point(), new Point(
DisplayShape.ActualWidth * scalingFactor.X / 2,
DisplayShape.ActualHeight * scalingFactor.Y / 2)));
TraceShape.RenderTransform = ScaleAtZeroRotateAtCenter(scaling, rotation, translation, DisplayShape.RenderSize, TraceShape.RenderTransformOrigin);
}
public static TransformGroup ScaleAtZeroRotateAtCenter(Vector scaling, double rotation, Vector translation, Size originalSize, Point renderTransformOrigin = default(Point))
{
var group = new TransformGroup();
var scaleTransform = new ScaleTransform
{
ScaleX = scaling.X,
ScaleY = scaling.Y,
CenterX = -originalSize.Width * renderTransformOrigin.X,
CenterY = -originalSize.Height * renderTransformOrigin.Y,
};
var rotateTransform = new RotateTransform
{
Angle = rotation,
CenterX = originalSize.Width * (scaling.X / 2 - renderTransformOrigin.X),
CenterY = originalSize.Height * (scaling.Y / 2 - renderTransformOrigin.Y),
};
group.Children.Add(scaleTransform);
group.Children.Add(rotateTransform);
group.Children.Add(new TranslateTransform {X = translation.X, Y = translation.Y});
return group;
}
考虑到前面可以灵活地运用得到的变换分量,我们现在也这么用:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private void OnLoaded(object sender, RoutedEventArgs args)
{
var matrix = DisplayShape.RenderTransform.Value;
var (scaling, rotation, translation) = TransformMatrix.MatrixToGroup(matrix,
scalingFactor => (new Point(), new Point(
DisplayShape.ActualWidth * scalingFactor.X / 2,
DisplayShape.ActualHeight * scalingFactor.Y / 2)));
TraceShape.Width = DisplayShape.ActualWidth * scaling.X;
TraceShape.Height = DisplayShape.ActualHeight * scaling.Y;
TraceShape.RenderTransform = NoScaleButRotateAtOrigin(
rotation, translation, DisplayShape.RenderSize);
}
public static TransformGroup NoScaleButRotateAtOrigin(double rotation, Vector translation, Size originalSize)
{
var group = new TransformGroup();
group.Children.Add(new RotateTransform {Angle = rotation});
group.Children.Add(new TranslateTransform {X = translation.X, Y = translation.Y});
return group;
}
我们的 RenderTransformOrigin 是随意设的,效果也像下图一样稳定可用。为了直观,我把两种用法放到了一起比较:
 ▲ 设置了
▲ 设置了 RenderTransformOrigin 依然有用
本文会经常更新,请阅读原文: https://blog.walterlv.com/post/extract-translation-scaling-rotation-from-matrix.html ,以避免陈旧错误知识的误导,同时有更好的阅读体验。
本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。欢迎转载、使用、重新发布,但务必保留文章署名 吕毅 (包含链接: https://blog.walterlv.com ),不得用于商业目的,基于本文修改后的作品务必以相同的许可发布。如有任何疑问,请 与我联系 ([email protected]) 。

