如果你试图通过 GetHashCode 得到的一个哈希值来避免冲突,你可能要失望了。因为实际上 GetHashCode 得到的只是一个 Int32 的结果,而 Int32 只有 32 个 bit。
32 个 bit 的哈希,有多大概率是相同的呢?本文将计算其概率值。
对于 GetHashCode 得到的哈希值,
- 9292 个对象的哈希值冲突概率为 1%;
- 77163 个对象的哈希值冲突概率为 50%。
计算方法
计算哈希碰撞概率的问题可以简化为这样:
- 有 1, 2, 3, … \(n\) 这些数字;
- 现在,随机从这些数字中取出 \(k\) 个;
- 计算这 \(k\) 个数字里面出现重复数字的概率。
例如:
- 有 1, 2, 3, 4 这四个不同的数字;
- 现在从中随机抽取 2 个。
那么抽取出来的可能的情况总数为:
\[4^2\]一定不会重复的可能的情况总数为:
\[4\times3\]意思是,第一次抽取的时候有 4 个数字可以选,而第二次抽取的时候就只有 3 个数字可以选了。
那么,会出现重复的概率就是:
\[1-\frac{4\times3}{4^2}\]也就是 25% 的概率会出现重复。
那么现在,我们随机抽取 3 个会怎样呢?
- 有 1, 2, 3, 4 这四个不同的数字;
- 现在从中随机抽取 3 个。
那么,会出现重复的概率就是:
\[1-\frac{4\times3\times2}{4^3}\]也就是 37.5%,64 种可能里面,有 24 种是有重复的。
现在,我们推及到 GetHashCode 函数的重复情况。
GetHashCode 实际上返回的是一个 Int32 值,占 32 bit。也就是说,我们有 \(2^{32}\) 个数字可以选。
现在问题是:
- 有 1, 2, 3, … \(2^{32}\) 这些数字,我们把 \(2^{32}\) 记为 \(n\);
- 现在从中随机抽取 \(k\) 个。
那么会出现重复的概率为:
\[1-\frac{n\times(n-1)\times(n-2)\times...(n-k+1)}{n^k}\]当然,分子分母都有的 \(n\) 可以约去:
\[1-\frac{(n-1)\times(n-2)\times...(n-k+1)}{n^{k-1}}\]计算的简化
而 \(k\) 很大的时候,此概率的计算非常复杂。然而我们可以取近似值简化成如下形式 [1]:
\[1-e^{\frac{-k(k-1)}{2n}}\]当然,实际上此计算在 \(k\) 取值较小的时候还可以进一步简化成:
\[\frac{k(k-1)}{2n}\]于是,在日常估算的时候,你甚至可以使用计算器估算出哈希值碰撞的概率。
你可以阅读 Hash Collision Probabilities 了解更多关于计算简化的内容。
概率图
为了直观感受到 32 bit 的哈希值的碰撞概率与对象数量之间的关系,我从 Socks, birthdays and hash collisions 和 Hash Collision Probabilities 找到了计算好的概率数据,并绘制成一张图:
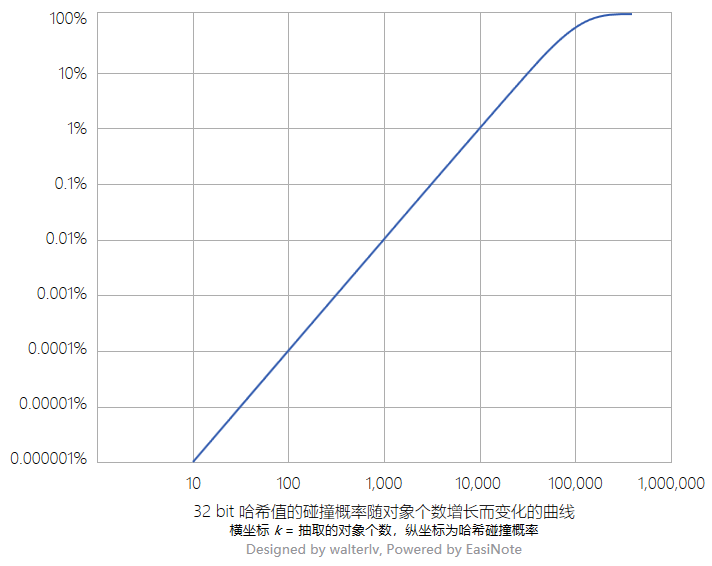
参考资料
- c# - Probability of getting a duplicate value when calling GetHashCode() on strings - Stack Overflow
- Socks, birthdays and hash collisions – Fabulous Adventures In Coding
- Hash Collision Probabilities
本文会经常更新,请阅读原文: https://blog.walterlv.com/post/hash-collisions-of-gethashcode.html ,以避免陈旧错误知识的误导,同时有更好的阅读体验。
本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。欢迎转载、使用、重新发布,但务必保留文章署名 吕毅 (包含链接: https://blog.walterlv.com ),不得用于商业目的,基于本文修改后的作品务必以相同的许可发布。如有任何疑问,请 与我联系 ([email protected]) 。

